Adversarially Constrained Autoencoder Interpolation (ACAI; Berthelot et al., 2018) is a regularization procedure that uses an adversarial strategy to create high-quality interpolations of the learned representations in autoencoders. This paper makes three main contributions:
- Proposed ACAI to generate semantically meaningful autoencoder interpolations.
- Developed a synthetic benchmark to quantify the quality of interpolations.
- Examined the performance of ACAI learned representations on downstream tasks.
AISC recently presented and discussed this paper led by Mahsa Rahimi. The details of the event can be found on the AISC website, and the full presentation can be viewed on YouTube. Here, we present an overview of the paper, along with the discussion points raised at the AISC session.
Interpolations in Autoencoders
Autoencoders are a class of neural nets that attempt to output an approximate reconstruction of an input with minimal information loss. As an autoencoder is trained, it learns to encode the input data into a latent space, capturing all the information needed to reconstruct the output. An autoencoder consists of two parts, an encoder and a decoder, which can be described as follows:
- The encoder receives the input data and generates a latent code .
- The decoder receives the latent code and attempts to reconstruct the input data as . The latent space is often of a lower dimension than the data ().
 The architecture of a standard autoencoder
The architecture of a standard autoencoder
Standard autoencoders focus on the reconstruction of the input and barely learn the probabilistic features of the underlying dataset. As a result, they have very limited generative power. One approach that allows standard autoencoders to generate synthetic data is to facilitate interpolation by mixing the latent codes. However, the latent space learned by a regular autoencoder might not be continuous and may have large gaps between clusters of latent codes. Simply mixing the previously learned latent codes may result in interpolations that fall into regions that the decoder has never seen before, which may result in the creation of unrealistic data points. To mitigate this, the interpolation process needs to be integrated into the autoencoder architecture and its training, allowing the autoencoder to learn the underlying data manifold and to create meaningful interpolations. By borrowing ideas from Generative Adversarial Networks (Goodfellow et al., 2014), ACAI effectively integrates the interpolation process into the autoencoder architecture. Berthelot et al. (2018) propose a method that can create high-quality interpolations that are both indistinguishable from real data, and are a semantically meaningful combination of the inputs. We explain the ACAI approach in detail below.
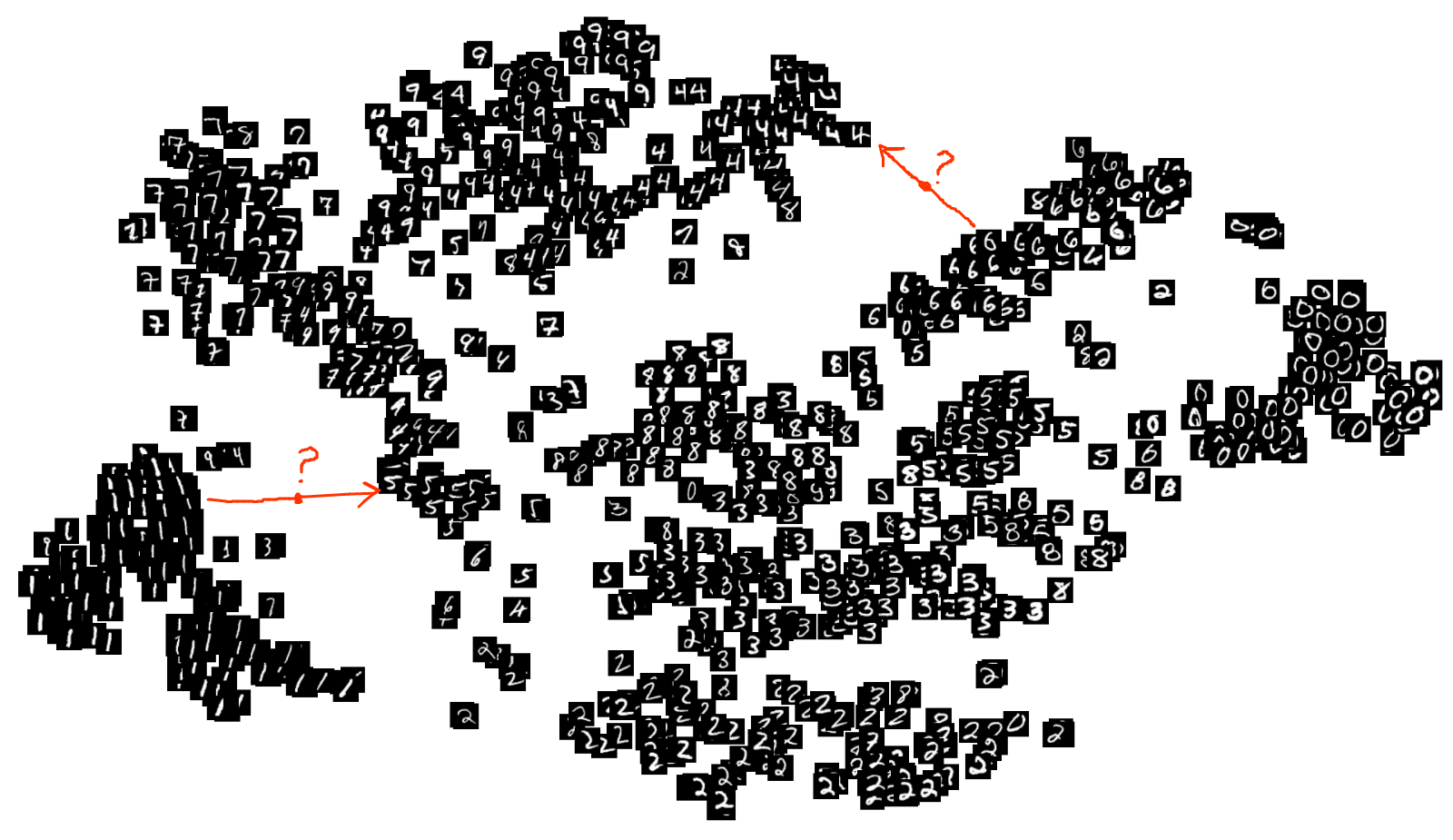 A visualization of the latent codes on the MNIST dataset showing the discontinuity of latent the space.
A visualization of the latent codes on the MNIST dataset showing the discontinuity of latent the space.
To read more on the continuity of the latent space you can read this blog post.
Adversarially Constrained Autoencoder Interpolation (ACAI)
To interpolate two inputs and , ACAI performs the following steps:
- Using two encoders, and are first encoded into the corresponding latent codes and where and .
- The two latent codes are then interpolated via a convex combination for some .
- The convex combination is then passed through a decoder to generate the interpolated data point, where .
- Finally, to ensure that interpolations are realistic, the decoded interpolation is passed through a critic network. The goal of the critic network is to predict the mixing coefficient from the interpolated data point . The autoencoder is then trained to fool the critic network into thinking that is always 0, meaning that it attempts to fool the critic network into thinking the interpolated data is actually non-interpolated.
Fooling the critic network is achieved by adding a term to the autoencoder's loss function. In ACAI, the encoders and the decoder are trained to minimize the following loss function:
where is a scalar hyperparameter that can be used to control the weight of the regularization term on the right, and is the critic network parametrized by . The first term of the loss function attempts to reconstruct the input, and the second term tries to make the critic network output 0 at all times. The critic network is trained to optimize the following loss function:
where is a scalar hyperparameter. The first term of the loss function attempts to recover . The second term is a regularization term that is not crucial for creating high-quality interpolations but helps with the adversarial learning process in two ways. First, it enforces the critic to consistently output 0 for non-interpolated data; and second, it ensures that the critic is exposed to realistic data even when the autoencoder reconstructions are of poor quality.
When the algorithm converges, the interpolated points are expected to be indistinguishable from real data. Empirically, the authors show that the learned interpolations are semantically smooth interpolations of the two inputs and . Evaluation results on a set of clustering and classification tasks show that the ACAI learned representations are more effective on downstream tasks than non-ACAI learned representations. Given the improved performance on the downstream tasks, the authors note that there may be a connection between interpolation and representation learning.
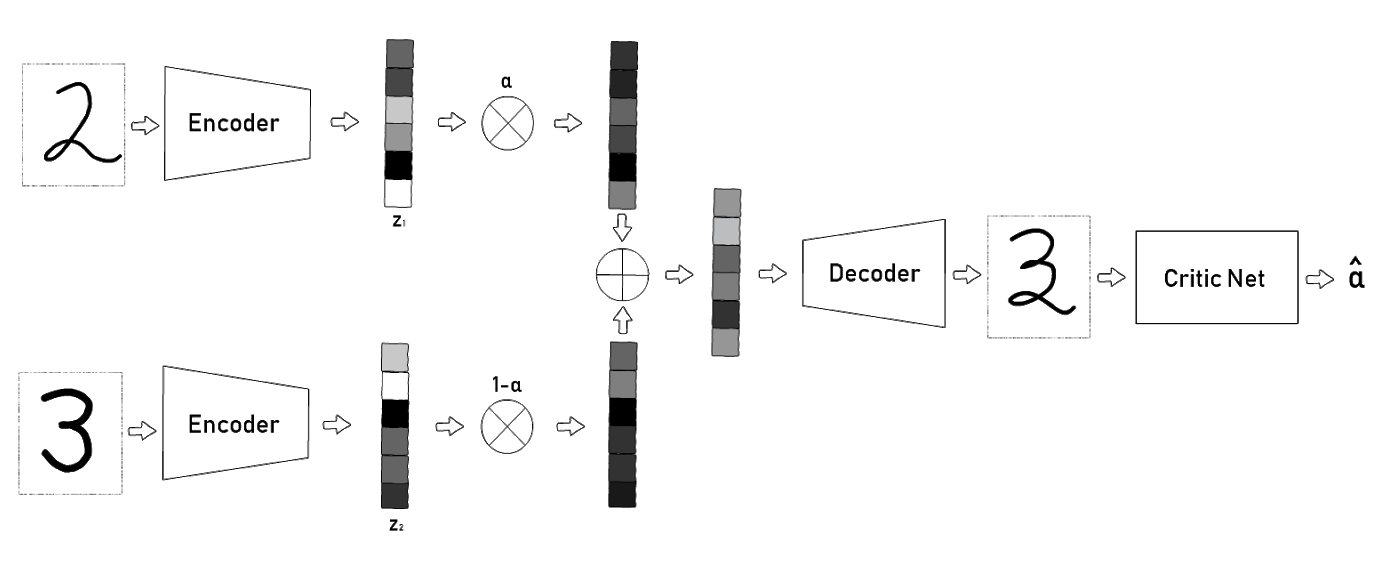 The ACAI Architecture
The ACAI Architecture
Benchmark Development
The concept of semantic similarity is ambiguous, ill-defined, and difficult to quantify. Another contribution of this paper is to define a benchmark to quantitatively evaluate the quality of interpolations. Their benchmark is focused on the task of autoencoding greyscale images of lines. The lines are -pixels long, beginning from the center of the image and extending outward at an angle , with a single line per image. Using this data, a valid interpolation between and is an image of a line that smoothly and linearly adjusts from the angle of the line in to the angle of the line in while traversing the shortest path. Using these images, the following two criteria can be easily calculated and are used to evaluate the interpolation capability of different autoencoders:
- Mean distance: measures the average distance between the interpolated points and real data points.
- Smoothness: measures whether the angles of the interpolated lines follow a linear trajectory between the start and endpoint.
An ideal interpolation would achieve 0 for both scores. An example of an ideal interpolation between and is shown below.
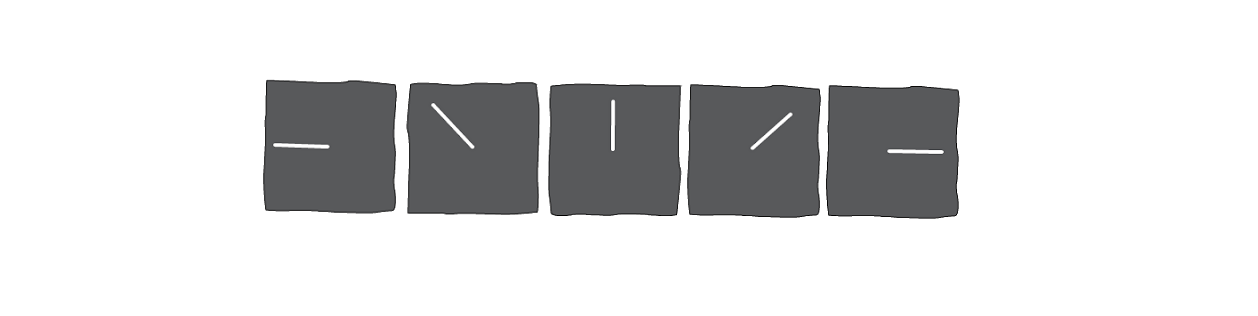 A perfect interpolation from to
A perfect interpolation from to
Using this benchmark, it is shown that ACAI substantially outperforms common autoencoder models (e.g., denoising and variational autoencoders) for the task of generating realistic and semantically meaningful interpolations.
AISC Discussions
In the AISC session, a set of discussion points were raised, which can be used as pointers for future work and experimentation on autoencoder interpolation.
First, the classification and clustering evaluations of ACAI representations are conducted on three different datasets: MNIST, SVHN, and CIFAR-10. While the results for both clustering and classification tasks are reasonable for the two simpler datasets (i.e., MNIST and SVHN), the classification improvement on CIFAR is not nearly as significant, and the CIFAR clustering outcome is poor for all of the autoencoders, including ACAI. AISC brought up the idea of extending ACAI to be more effective on complicated datasets.
Second, the ACAI paper primarily focuses on computer vision tasks and even defines high-quality interpolations based on visual attributes of images. It would be extremely valuable to explore how ACAI and the benchmark could be extended to benefit non-visual tasks such as text interpolation. Finally, in this paper, the regularization procedure is applied to a vanilla autoencoder. It would be worth exploring the effects of using a similar regularization mechanism on other types of autoencoders. In particular, the possibility of improving the generative power of variational autoencoders using the same idea was discussed in the AISC session.
Additional Resources: